计图(Jittor)是清华大学自主研发的深度学习框架,自2020年3月发布以来,因为元算子融合和统一计算图的两大创新,在很多应用领域,取得了优于国际主流框架的性能。
近期,南开大学程明明教授团队开源了基于Jittor的语义线检测算法,称为“深度霍夫变换”(deep hough transform,简称 DHT),该成果发表于IEEE T-PAMI。基于Jittor的DHT算法相比于PyTorch,网络推理性能大幅提升,采用RTX TITAN显卡,在batch size为8时,能达到3.12倍的加速。
DHT算法通过在深度特征上进行霍夫变换,从而兼顾CNN的特征学习能力和霍夫变换的高效性[1]。作者还发布了一个包含室内/室外场景的大型语义线检测数据集 NKL (NanKai Lines)。NKL数据集有6,500张图像以及超过1万根语义线标注,为该领域目前最大的公开数据集。
图像中的语义线
图像中直线(线段)的检测是一个经典的计算机视觉问题,图像中的线结构是一种有用的中间层表示,在人类视觉中从底层到高层的语义信息转换中有着重要作用 [2]
自然图像中的“语义线”指的是图像中能够勾勒出图像内容结构的直线,例如不同区域的分割线,建筑物的中轴线等。语义线检测[3]在摄影构图[4,5],图像处理[6]等多种任务中有着广泛应用。如图1所示,将图像中的语义线置于照片的黄金分割比位置能拍出视觉效果更好的效果 [4]。
图1:左图为原图,右图将语义线置于画面的黄金分割比位置,能得到更好的视觉效果*[3]*
深度霍夫变换算法DHT
霍夫变换[6]是一种经典的直线检测算法,通过将任意直线转换到参数空间,将图像空间的线检测问题简化为参数空间的点检测问题。例如,平面上的任意直线都可以用 y = k x + b 来表示,因此任意一条直线都可以表示为参数空间中的一个点(k, b)。
传统的霍夫变换需要先用边缘检测算法(例如canny算子)对图像进行边缘检测,然后在边缘检测的结果之上进行霍夫变换,最后在变换空间通过寻找局部最大值来检测直线。
直线参数化
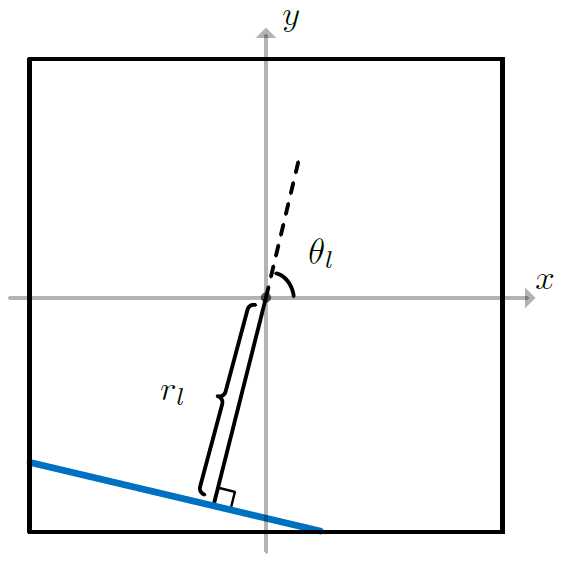
为了进行霍夫变换,首先要定义直线参数化的规则。
图2:直线的参数化
如上图所示,对任意一条直线,用其角度 theta 和直线到原点的距离 r 作为直线的参数,从而可以参数化任意角度/位置的直线 (用y = kx + b 无法参数化与 y 轴平行的直线)。
在深度特征上进行霍夫变换
如图3所示,对于一个输入图片,先通过CNN 特征提取器得到空间特征X,“深度霍夫变换”遍历图像中所有可能的直线并沿着直线将特征聚合到参数空间中对应的点上。在实现中,使用简单的求和操作实现特征聚合。
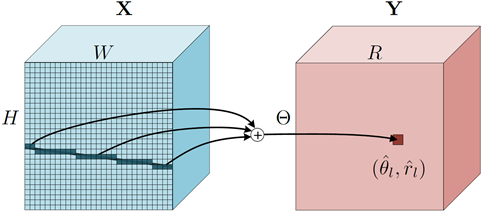
图3 左:深度霍夫变换沿着图像空间中的直线将特征”聚合“到参数空间中的一个点
经过深度霍夫变换,原特征空间 X 上的一根直线对应参数空间 Y 上的一个点。在很多视觉任务中,特征的上下文(context)对于检测结果十分重要,深度霍夫变换将直线转化为点,因此提取相邻直线的上下文信息对应于在参数空间中提取相邻点的特征,大大简化了上下文信息提取的效率。
如图4所示,在原图像中提取橙色线的上下文信息需要复杂的索引操作;经过霍夫变换之后,只需要一个简单的 3x3 卷积即可提取中心线周围直线的特征。
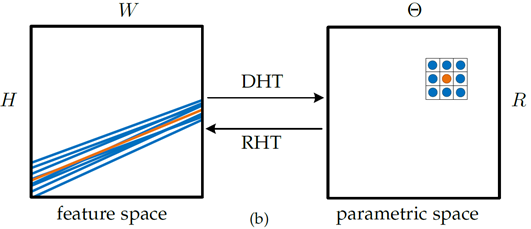
图4:图像空间中的线对应参数空间的一个点
总的来说,深度霍夫变换算法有如下几个优点:
- 高度可并行化,相比基于目标检测的SLNet方法加速了接近20 倍;
- 极大简化了非极大值抑制;
- 高效的上下文直线信息提取。
实验结果
定量对比
程明明教授团队主要在 SEL 和 NKL 数据集上进行了试验,对比了 HED边缘检测 + 霍夫变换,SLNet 两种语义线检测方法。实验结果表明DHT算法检测精度显著高于其他两种算法,同时大幅提高检测速度。
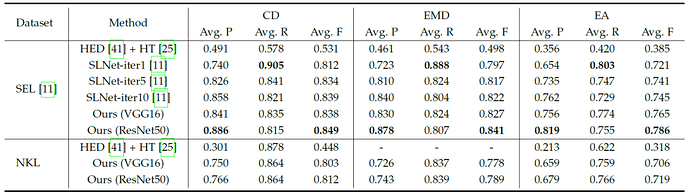
表1 不同方法在数据集上的定量对比
表1记录了不同方法在 SEL 和 NKL 数据集上的定量对比。CD,EMD 和 EA 分别指的是 Chamfer distance, earth-mover’s distance 和 EA-score 三种评价直线之间相似度的度量。Avg P, R, F分别表示平均 precision,recall 和 F-measure。
可视化结果展示
下图是SEL数据集上不同方法检测结果的可视化对比,最后一行为 ground-truth.
图5 SEL数据集上的可视化对比
推理时间的对比
DHT算法不仅能取得更高的检测精度,同时也能极大地降低检测耗时。这主要归功于 DHT 算法的高度可并行化。
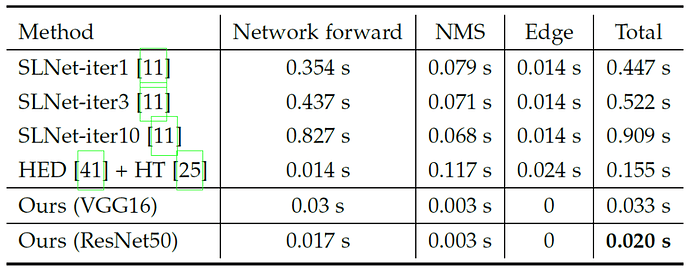
下表统计了不同方法在 RTX 2080Ti显卡上的平均推理耗时,SLNet 最快需要0.447秒,HED+霍夫变换的方法需要0.155秒,而DHT 算法仅需0.020秒。
表2 RTX 2080Ti显卡上的平均推理时间
语义线检测数据集NKL
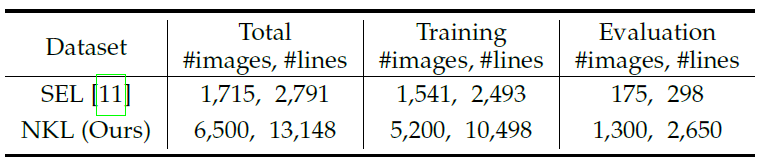
该论文在提出深度霍夫变换算法的同时,还构建了新的语义线检测数据集 NKL (NanKai Lines)。NKL数据集包含6,500张样本,共有13,148根人工标注的语义线。相比当前最大的语义线检测数据集 SEL,NKL不论是在样本数,标注数目还是场景多样性上都要更丰富。
表3:SEL 数据集和 NKL 数据集对比
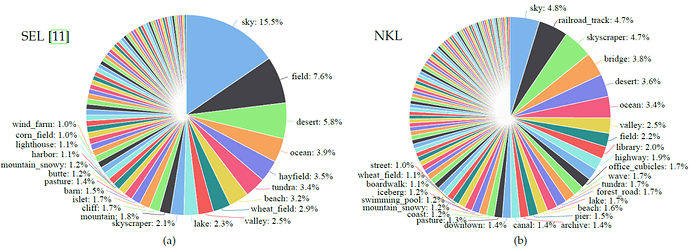
为了验证 NKL 数据集在图像场景中的多样性,该论文使用在 Places365 数据集上预训练的模型分别对 NKL 和 SEL 数据集中的样本进行推理,预测的分类结果如图5所示。
图5:SEL和论文新构建的 NKL 数据集的场景分布
从上图可以看出,SEL 的大部分样本集中在天空、场地等少数场景,而NKL数据集中样本的分布更为多样化,同时场景类别也更多。
Jittor框架大幅提升推理速度
该论文提供了基于清华大学自主研发的“计图” (Jittor) 框架的推理代码,得益于Jittor框架“元算子融合”和“统一计算图”两项新技术[8],DHT 算法无需任何优化情况下推理速度相比PyTorch 就有显著提升。
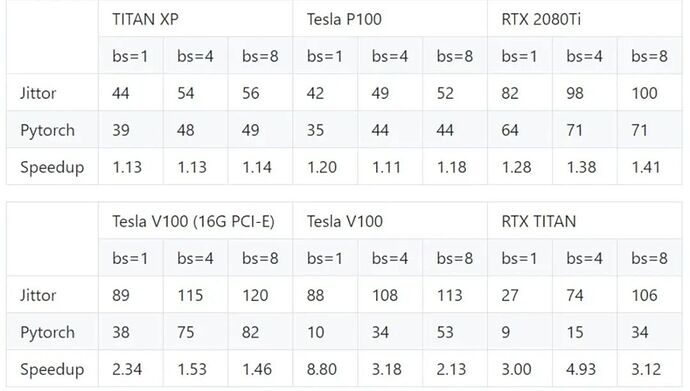
下表给出了不同显卡上,Jittor框架和PyTorch框架对前向预测的性能对比。
表3:SEL 数据集和 NKL 数据集对比
可以看到,在TITAN XP和Tesla P100上,Jittor平均有1.15左右的加速, 而在Tesla V100、RTX TITAN等新款的显卡上,针对不同的batch size,几乎都有两三倍的加速,其中RTX TITAN在batch size为8时,能达到3.12倍的加速。
针对DHT算法在不同硬件上的性能差异较大的问题,经过研究发现,原因在于DHT算法基于Jittor和PyTorch开发自定义算子时,使用到了不同的CUDA运行时函数,该运行时函数在不同硬件的上效率差异较大。Jittor开发的自定义算子代码更精简,效率更高,同时计算结果与PyTorch一致。
DHT算法的项目主页:
DHT算法的GitHub开源:
参考文献
- Kai Zhao, Qi Han, Chang-Bin Zhang, Jun Xu, Ming-Ming Cheng, Deep Hough Transform for Semantic Line Detection, IEEE T-PAMI, 2021.
- J. B. Burns, A. R. Hanson, and E. M. Riseman, Extracting straight lines, IEEE T-PAMI, Vol. 8, No. 4, 425–455, 1986.
- J.-T. Lee, H.-U. Kim, C. Lee, and C.-S. Kim, Semantic line detection and its applications, ICCV, 2017, 229–3237.
- L. Liu, R. Chen, L. Wolf, and D. Cohen-Or, Optimizing photo composition, Computer Graphics Forum, Vol. 29, No. 2, 469–478, 2010.
- M. Freeman, The photographer’s eye: composition and design for better digital photos, CRC Press, 2007
- M.-M. Cheng, X.-C.Liu, J. Wang, S.-P. Lu, Y.-K. Lai, and P. L. Rosin, Structure-preserving neural style transfer, IEEE TIP, Vol. 29, 909–920, 2020.
- R. O. Duda and P. E. Hart, Use of the hough transformation to detect lines and curves in pictures, Sri International Menlo Park Ca Artificial Intelligence Center, Tech. Rep., 1971.
- S.-M. Hu, D. Liang, G.-Y. Yang, G.-W. Yang, W.-Y. Zhou, Jittor: a novel deep learning framework with meta-operators and unified graph execution, Science China Information Sciences, Vol. 63, No.12, 2020, 222103:1-21.