最近在研究SubdivNet这篇论文的代码,遇到了一些问题。
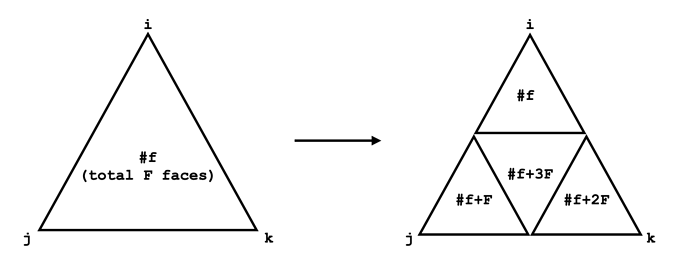
三维网格在经过卷积之后就会进入池化层,在池化层中,四个面合成一个面,然后选四个面中最大的特征作为新的面的特征。
附上这段代码:
def inverse_loop_pool(self, op='max', pooled_feats=None):
"""
Pooling with the inverse loop scheme.
Parameters:
------------
op: {'max', 'mean'}, optional
Reduction method of pooling. The default is 'max'.
pooled_feats: (N, C, F) float32, optional
Specifying the feature after pooling.
Returns:
------------
MeshTensor after 4-to-1 face merge.
"""
pooled_Fs = self.Fs // 4
pooled_faces = self.faces.reindex(
shape=[self.N, self.F // 4, 3],
indexes=[
'i0',
'i1 + @e0(i0) * i2',
'0',
],
extras=[pooled_Fs],
overflow_conditions=['i1 >= @e0(i0)'],
overflow_value=0
)
if pooled_feats is None:
pooled_feats = self.feats.reindex(
shape=[self.N, self.C, self.F // 4, 4],
indexes=[
'i0',
'i1',
'i2 + @e0(i0) * i3'
],
extras=[pooled_Fs],
overflow_conditions=['i2 >= @e0(i0)'],
overflow_value=0
)
if op == 'max':
pooled_feats = jt.argmax(pooled_feats, dim=3)[1]
elif op == 'mean':
pooled_feats = jt.mean(pooled_feats, dim=3)
else:
raise Exception('Unsupported pooling operation')
else:
assert pooled_feats.shape[0] == self.N
assert pooled_feats.shape[2] == self.F // 4
return MeshTensor(pooled_faces, pooled_feats, pooled_Fs)
这段代码中self.faces.reindex()方法就是四个面合成一个面,以下是我对这个方法的解读:
(用的数据集是cubes)
for i0 in range(shape[0]):
for i1 in range(shape[1]):
for i2 in range(shape[2]):
y[i0,i1,i2]=x[i0,i1+@e0(i0)*i2,0]
x是输入的faces,y是输出的faces。
y[0,0,0]=x[0,0,0]=4
y[0,0,1]=x[0,3072,0]=414
y[0,0,2]=x[0,6144,0]=413
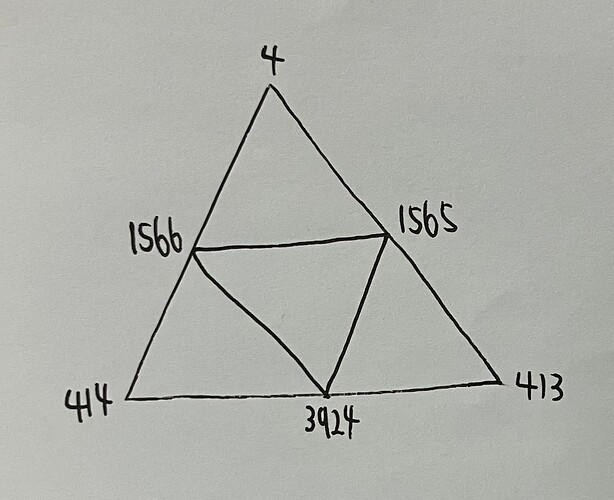
也就是说,池化后的faces中的第一个三角面片是由4,414,413这三个点构成的,而这三个点又是从原来的faces中每隔3072(12288//4=3072)个取得的。那么问题就来了,怎么可以确定4,414,413这三个点在网格中的位置是刚好间隔一个点位呢?万一它们仨在网格中的位置离得很远呢?
于是我查看了网格原来的faces,分别查了第0个面,第3072个面,第6144个面,第9216个面,是由哪三个点组成的,以下是查到的结果:
0: 4 1566 1565
3072:414 3924 1566
6144:413 1565 3924
9216:3924 1565 1566
这四个面分别相隔3072个索引,然后在三维网格上它们又能组成一个大的三角面片,如下图:
我现在觉得好神奇,想知道这些面片的排序方式是怎样规定的?是人为排序的吗?但我在SubdivNet中并没有找到生成faces的代码。
(如果我没有把问题说明白的话,我再完善一下。)