计图开源:纹理网格模型生成方法TM-NET
近期中科院计算所高林团队和SFU的张皓教授、英国卡迪夫大学来煜坤教授合作,在计算机图形学顶会ACM SIGGRAPH Asia 2021上发表纹理网格模型生成方法TM-NET[1],并在计图框架上开源。
三维模型的建模一直是计算机图形学领域的一个热门方向,近些年来许多的研究者尝试将深度网络应用于三维模型的生成上。例如基于点云、体素、片网、隐式函数、网格等表示的一系列方法,但这些方法都仅仅考虑了三维模型的几何建模,生成的模型都是“光秃秃”的,而工业界的应用往往需要带纹理的三维模型,这是因为纹理可以有效增强三维模型的真实感,如图1所示,可以通过透明通道巧妙表达空洞拓扑结构。
图1 左:没有纹理的三维模型;右:TM-NET生成三维模型的纹理
在深度三维模型分析合成方向,已有三维模型变形传播[2]、三维模型编辑[3]、和人造模型合成[4]的工作,为了进一步生成结构化并带纹理的三维模型,中科院计算所高林团队和SFU的张皓教授、英国卡迪夫大学来煜坤教授等合作,提出了一种能够表达精细几何和高质量纹理的三维模型深度生成方法TM-NET[1]。该方法能够通过从三维模型数据库中学习数据分布特征,并生成相应的带纹理的三维模型,减少了建模三维模型的工作量。
Part 1
带纹理模型的深度学习表示
纹理作为一种增强三维模型细节和真实度的方法,很早便受到了关注。1974年,图灵奖得主Edwin Catmull提出了纹理映射,提供了将二维图像映射到三维模型的方法来增强渲染的真实感。1985年Perlin发表于SIGGRAPH的文章[5]中提出自动生成随机纹理,2015年清华大学胡事民教授团队发表于ACM SIGGRAPH Asia的MagicDecorator[6]提出针对复杂场景自动纹理生成的新方法。然而针对复杂人造三维模型(如图2),其纹理映射往往十分复杂,需要人工指定纹理坐标,这一过程耗时耗力。

图2 将三维模型映射到二维平面的过程
直接对模型整体建模比分块建模更困难。为了减少手工交互,加快建模速度,同时实现高质量的三维模型生成,受作者之前 SDM-NET[4]工作启发,该方法将完整的模型分割为具有特定语义标签的部件,逐一对每个部件进行建模。其核心思想为用多个同拓扑的包围盒表示带纹理的三维模型的不同部件,而包围盒的纹理展开方式则十分简单自然。
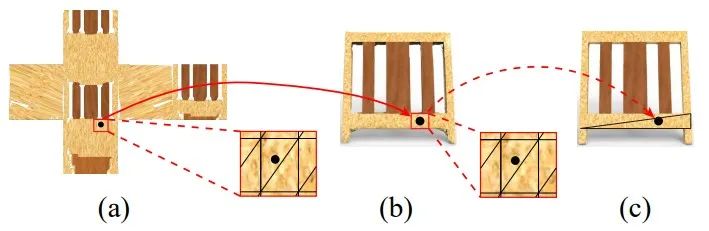
例如图3,给定一个带纹理的椅背,该方法使用一个包围盒对其进行注册,然后通过光线追踪找最近点的方式将纹理从原始的带纹理的三维模型传播到变形后的包围盒上,其纹理传播流程如图4所示,其中(a)为包围盒的纹理展开,(b)为带纹理的变形包围盒,(c)为数据库中的原始模型,通过从变形包围盒(b)上向原始模型(c)上发射光线的方式可以得到纹理展开图(a)相应位置的纹理颜色。这样每个标签部件的几何集合对应一个同胚集合,同时每个标签部件的纹理也都映射到了同一个对齐的二维平面。

图3 最左为原始模型,中间一列为初始包围盒以及二维展开,最右为变形后包围盒以及其二维纹理展开
图4 纹理传播流程
此外,为了解决三维模型上的孔洞等复杂拓扑难以刻画的问题,该方法利用纹理作为媒介,用纹理图片的透明通道来表示几何。如图5所示,原始的三维模型并没有孔洞,通过给三维模型贴透明纹理的方式,无需修改原三维模型的网格连接关系,就能表达椅背上的复杂几何拓扑。
图5 透明纹理表示椅背上复杂的孔洞拓扑
Part 2
TM-NET算法原理
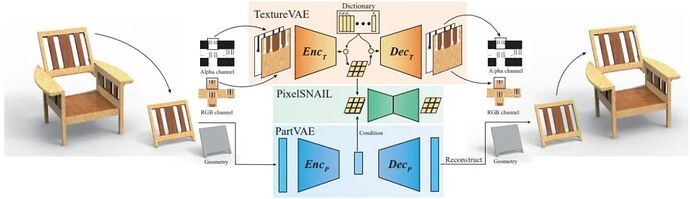
如图6所示,TM-NET主要由三个模块组成:纹理变分自编解码器(TextureVAE)、几何变分自编解码器(PartVAE)以及自回归模型(PixelSNAIL)组成。几何变分自编解码器和纹理变分自编解码器分别用于编码三维模型的几何形变和纹理图片,而自回归模型则负责学习给定几何条件下纹理数据的分布。
图6 TM-NET网络架构
纹理变分自编码器将纹理图片作为输入,将其编码到特征向量上,并通过解码器解码重建图片。其损失函数包括图像重建损失、特征向量量化重建损失和纹理图展开边界损失,保证了图片重建质量、量化前后的特征向量尽可能相近以及纹理图展开边界上不出现瑕疵。
对于几何变分自编码器,其将包围盒的变形特征[7]作为输入,将其编码到固定长度的隐含层,再通过解码器解码恢复。其损失函数包括变形特征的重建损失、隐含层的KL损失。保证了网络的编码能力和隐含层的分布近似于高斯分布。
训练完纹理变分自编码器和几何变分自编码器后,可以完成带纹理的三维模型的重建和插值等应用。而对于生成应用,需要训练自回归模型来学习几何和纹理之间的关系。自回归模型通过学习给定条件下,当前像素和之前像素的条件概率分布,可以计算得到整个图像的概率分布,从而实现自回归的采样生成。自回归模型的输入有两个,一个是几何变分自编码器的隐含层向量作为条件输入,另一个是纹理变分自编码器的特征向量。其损失函数为交叉熵损失。训练完成后可以通过自回归采样生成纹理变分自编码器的特征向量,并使用解码器解码得到纹理。
Part 3
更多的结果展示和应用
下面给出几个效果的展示。如图7所示,通过纹理的透明通道表示复杂的几何细节,在重建质量上,TM-NET具有优势。
图7 与基于隐式场(IM-NET,BSP-NET)、网格(SDM-NET)表示方法的比较,最左为输入的三维模型,其他为不同方法使用网络重建的结果
给定一个三维模型,将其转化为该方法表示方式,再通过自回归模型进行纹理的合成,可以看到生成的纹理可以契合输入三维模型,结果如图8所示。
图8 最左为没有纹理的三维模型,其他为经过多次采样生成得到的带纹理的三维模型
同样的,通过直接在几何变分自编解码器的隐空间中采样,再将其作为条件输入到自回归模型中进行纹理的合成,同样可以生成合理的带纹理的三维模型,生成结果如图9所示。
图9 随机生成带纹理的三维模型
文章对于纹理展开边界损失进行了实验评估,结果如图10所示,可以看到在不带纹理展开边界损失的实验结果中,边界处出现了相应的瑕疵,而在带纹理展开边界损失的实验结果中则没有这种现象。
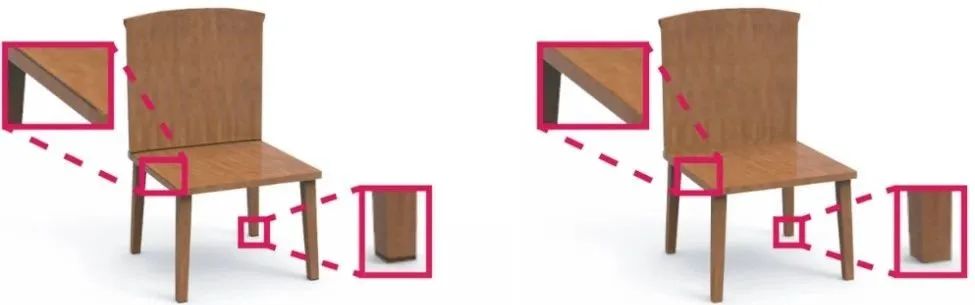
图10 不带纹理展开边界损失(左)和带纹理展开边界损失(右)对比
目前TM-NET已经发布基于计图(Jittor)的版本,Jittor是清华大学计算机图形学实验室开源的自主深度学习框架。
开源代码见:
基于计图实现的代码训练速度是Pytorch版本的1.32倍,推理速度是Pytorch版本的2.94倍。
参考文献
- Lin Gao, Tong Wu, Yu-Jie Yuan, Ming-Xian Lin, Yu-Kun Lai, and Hao Zhang, TM-NET: Deep Generative Networksfor Textured Meshes, ACM Transactions on Graphics, 2021, Vol. 40, No. 6, 263:1-263:15.
- Lin Gao, Jie Yang, Yi-Ling Qiao, Yu-Kun Lai, Paul L.Rosin, Weiwei Xu, and Shihong Xia, Automatic unpaired shape deformation transfer, ACM Transactions on Graphics, 2018, Vol. 37, No. 6, 237:1–237:15.
- Qingyang Tan#, Ling-Xiao Zhang#, Jie Yang, Yu-Kun Lai, and Lin Gao*, Mesh-based VariationalAutoencoders for Localized Deformation Component Analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 10.1109/TPAMI.2021.3085887.
- Lin Gao, Jie Yang, Tong Wu, Yu-Jie Yuan, Hongbo Fu, Yu-Kun Lai, and Hao Zhang, SDM-NET: Deep Generative Network for Structured Deformable Mesh, ACM Transactions on Graphics, 2019, Vol. 38, No. 6, 243:1-243:15.
- Ken Perlin, An image synthesizer, ACM Transactions on Graphics, 1985, Vol.19, No. 3, 287–296.
- Kang Chen, Kun Xu, Yizhou Yu, Tian-Yi Wang and Shi-Min Hu, Magic decorator: automatic material suggestion for indoor digitalscenes, ACM Transactions on Graphics, 2015, Vol. 34, No. 6, 232:1–232:11.
- Lin Gao, Yu-Kun Lai, Jie Yang, Ling-Xiao Zhang, Shihong Xia, and Leif Kobbelt, Sparse Data Driven Mesh Deformation, IEEE Transactions on Visualization and Computer Graphics, 2019, Vol. 27, No. 3, 2085-2100.